Lessons learned in high-performance R

On this blog, I’ve had a long running investigation/demonstration of how to make a “embarrassingly-parallel” but computationally intractable (on commodity hardware, at least) R problem more performant by using parallel computation and Rcpp.

The example problem is to find the mean distance between every airport in the United States. This silly example was chosen because it exhibits polynomial growth in running time as a function of the number of airports and, thus, quickly becomes intractable without sampling. It is also easy to parallelize.

TODO The first post used the (now-deprecated in favor of ‘parallel’) multicore package to achieve a substantial speedup. The second post used Rcpp to achieve a statistically significant but, functionally, trivial speedup by replacing the inner loop (the distance calculation using the Haversine formula) with a version written in C++ using Rcpp. Though I was disappointed in the results, it should be noted that porting the function to C++ took virtually no extra work.

By necessity, I’ve learned a lot more about high-performance R since writing those two posts (part of this is by trying to make my own R package as performant as possible). In particular, I did the Rcpp version all wrong, and I’d like to rectify that in this post. I also compare the running times of approaches that use both parallelism and Rcpp.

###Lesson 1: use Rcpp correctly

The biggest lesson I learned, is that it isn’t sufficient to just replace inner loops with C++ code; the repeated transferring of data from R to C++ comes with a lot of overhead. By actually coding the loop in C++, the speedups to be had are often astounding.

In this example, the pure R version, that takes a matrix of longitude/latitude pairs and computed the mean distance between all combinations, looks like this…

1
2
3
4
5
6
7
8
9
10
11
12
just.R <- function(dframe){
  numrows <- nrow(dframe)
  combns <- combn(1:nrow(dframe), 2)
  numcombs <- ncol(combns)
  combns %>%
    { mapply(function(x,y){
        haversine(dframe[x,1], dframe[x,2],
                  dframe[y,1], dframe[y,2]) },
        .[1,], .[2,])} %>%
    sum %>%
    (function(x) x/(numrows\*(numrows-1)/2))
}

The naīve usage of Rcpp (and the one I used in the second blog post on this topic) simply replaces the call to “haversine” with a call to “haversine_cpp”, which is written in C++. Again, a small speedup was obtained, but it was functionally trivial.

The better solution is to completely replace the combinations/“mapply” construct with a C++ version. Mine looks like this…

1
2
3
4
5
6
7
8
9
10
11
12
double all_cpp(Rcpp::NumericMatrix& mat){
    int nrow = mat.nrow();
    int numcomps = nrow*(nrow-1)/2;
    double running_sum = 0;
    for( int i = 0; i < nrow; i++ ){
        for( int j = i+1; j < nrow; j++){
            running_sum += haversine_cpp(mat(i,0), mat(i,1),
                                         mat(j,0), mat(j,1));
        }
    }
    return running_sum / numcomps;
}

The difference is incredible…

1
2
3
4
5
6
7
8
9
10
res <- benchmark(R.calling.cpp.naive(air.locs[,-1]),
                 just.R(air.locs[,-1]),
                 all_cpp(as.matrix(air.locs[,-1])),
                 columns = c("test", "replications", "elapsed", "relative"),
                                  order="relative", replications=10)
res
#                                   test replications elapsed relative
# 3  all_cpp(as.matrix(air.locs[, -1]))           10   0.021    1.000
# 1 R.calling.cpp.naive(air.locs[, -1])           10  14.419  686.619
# 2              just.R(air.locs[, -1])           10  15.068  717.524

The properly written solution in Rcpp is 718 times faster than the native R version and 687 times faster than the naive Rcpp solution (using 200 airports).

Lesson 2: Use mclapply/mcmapply

In the first blog post, I used a messy solution that explicitly called two parallel processes. I’ve learned that using mclapply/mcmapply is a lot cleaner and easier to intregrate into idiomatic/functional R routines. In order to parallelize the native R version above, all I had to do is replace the call to “mapply” to “mcmapply” and set the number of cores (now I have a 4-core machine!).

Here are the benchmarks:

1
2
3
4
5
                                           test replications elapsed relative
2 R.calling.cpp.naive.parallel(air.locs[, -1])           10  10.433    1.000
4              just.R.parallel(air.locs[, -1])           10  11.809    1.132
1          R.calling.cpp.naive(air.locs[, -1])           10  15.855    1.520
3                       just.R(air.locs[, -1])           10  17.221    1.651

Lesson 3: Smelly combinations of Rcpp and parallelism are sometimes counterproductive

Because of the nature of the problem and the way I chose to solve it, the solution that uses Rcpp correctly is not easily parallelize-able. I wrote some *extremely* smelly code that used explicit parallelism to use the proper Rcpp solution in a parallel fashion; the results were interesting:

1
2
3
4
5
6
7
                                          test replications elapsed relative
5           all_cpp(as.matrix(air.locs[, -1]))           10   0.023    1.000
4              just.R.parallel(air.locs[, -1])           10  11.515  500.652
6             all.cpp.parallel(air.locs[, -1])           10  14.027  609.870
2 R.calling.cpp.naive.parallel(air.locs[, -1])           10  17.580  764.348
1          R.calling.cpp.naive(air.locs[, -1])           10  21.215  922.391
3                       just.R(air.locs[, -1])           10  32.907 1430.739

The parallelized proper Rcpp solution (all.cpp.parallel) was outperformed by the parallelized native R version. Further the parallelized native R version was much easier to write and was idiomatic R.

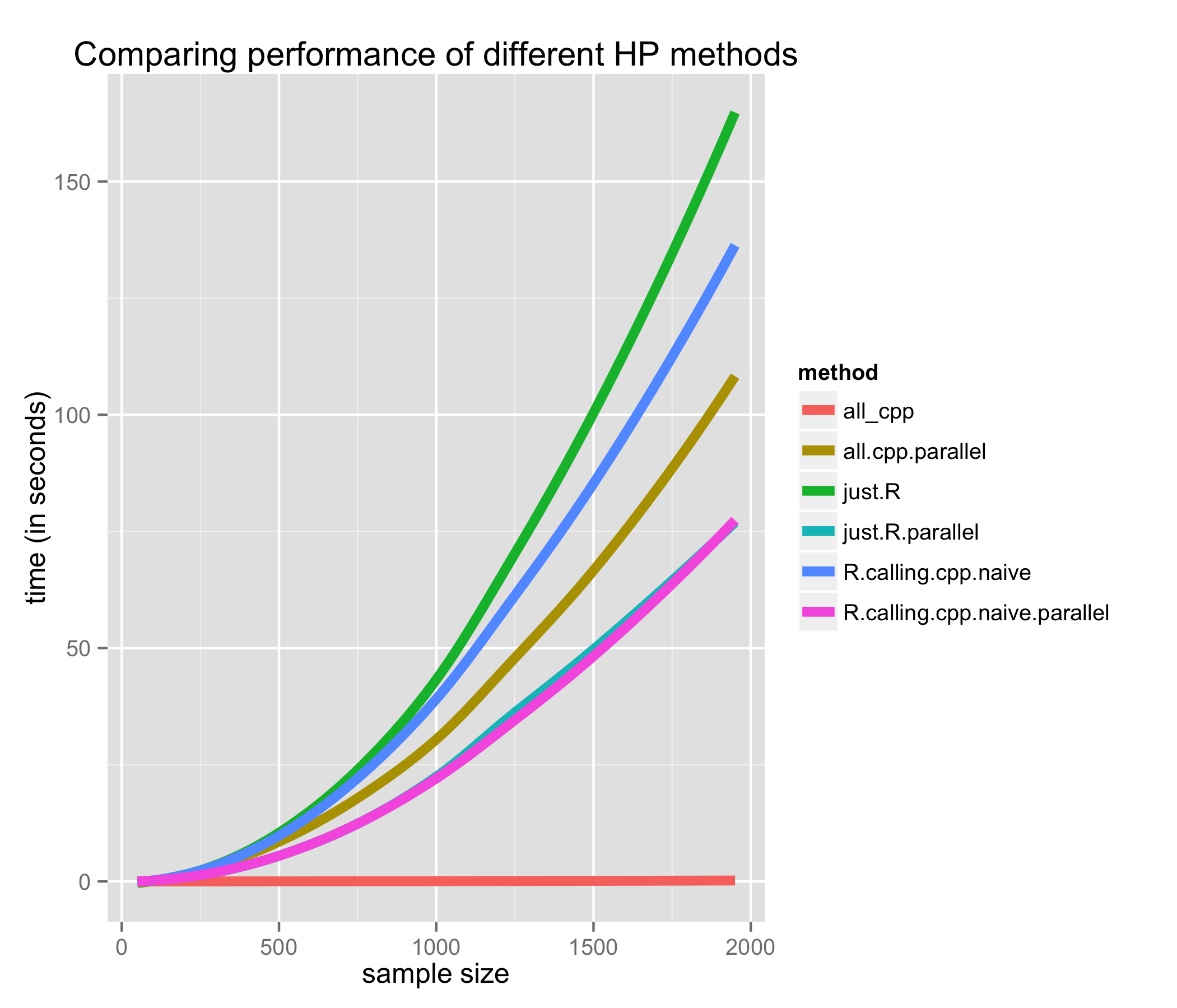
How does it scale?

Comparing performance of different HP methods

Two quick things…

  • The “all_cpp” solution doesn’t appear to exhibit polynomial growth; it does, it’s just so much faster than the rest that it looks completely flat

  • It’s hard to tell, but that’s “just.R.parallel” that is tied with “R.calling.cpp.naive.parallel”

Too long, didn’t read: If you know C++, try using Rcpp (but correctly). If you don’t, try multicore versions of lapply and mapply, if applicable, for great good. If it’s fast enough, leave well enough alone.

PS: I way overstated how “intractable” this problem is. According to my curve fitting, the vanilla R solution would take somewhere between 2.5 and 3.5 hours. The fastest version of these methods, the non-parallelized proper Rcpp one, took 9 seconds to run. In case you were wondering, the answer is 1,869.7 km (1,161 miles). The geometric mean might have been more meaningful in this case, though.